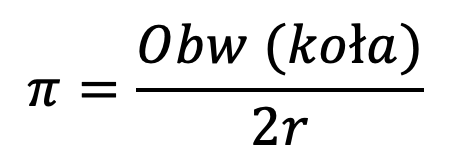Konwerter obrazu na tekst to program zamieniający piksele w pliku graficznym na tekst wyrażony znakami ascii w notatniku. Co prawda taka aplikacja nie ma zbyt wielu zastosowań, ale stanowi miłe, krótkie ćwiczenie w operowaniu na obrazie oraz plikach. Dla przykładu tak wygląda działanie omawianego programu.
Czytaj dalej Konwerter obrazu na tekst z pomocą królowej naukTag: matematyka
Wzory jako fundamenty mechaniki gier komputerowych
Gry komputerowe to niezwykle złożone programy. Ich proces tworzenia wymaga wielu godzin myślenia nad najróżniejszymi aspektami. Rozgrywka, fabuła i klimat – to tylko niektóre z nich, a każde wymaga uprzedniego zaprojektowania.
Czytaj dalej Wzory jako fundamenty mechaniki gier komputerowychMatematyka w justowaniu
Byłbym w stanie zaryzykować stwierdzenie, że każda aplikacja, która komunikuje się z użytkownikiem za pomocą interfejsu, zawiera w sobie tekst.
Chcąc by z naszych programów korzystało się z uśmiechem na ustach, powinniśmy przestrzegać pewnych zasad estetyki, a umiejętność wyrównywania tekstu z pewnością w tym pomoże.
Czytaj dalej Matematyka w justowaniuPrawdopodobieństwo jako podstawa sztucznej inteligencji w grze z elementami RNG
Podejmowanie decyzji to niekiedy bardzo ciężki i złożony proces. Jako że nam ludziom często zdarza się stawać w sytuacjach w których musimy wybierać, opanowaliśmy tę umiejętność naprawdę porządnie. Komputer jednak wykonuje tylko nasze polecenia, więc jego poziom samodzielnego podejmowania decyzji jest zerowy. To my musimy poinstruować naszą sztuczną inteligencje jakie kroki będzie miała podjąć, by osiągnąć oczekiwany rezultat. Pomijamy tu oczywiście algorytmy samouczące, które korzystając z wcześniej przygotowanych materiałów szkoleniowych, opracowują odpowiedni schemat działań. My skupimy się na prostym algorytmie opartym na drzewie zachowań, w którym to my będziemy musieli krok po kroku określić zachowania sztucznej inteligencji.
Czytaj dalej Prawdopodobieństwo jako podstawa sztucznej inteligencji w grze z elementami RNGMatematyka w programowaniu – wstęp
Jako, że obecny rok został ustanowiony rokiem matematyki podjęte zostały liczne inicjatywy mające na celu pokazanie jak ważna jest królowa nauk w naszym życiu. Ja kierując się podobnym myśleniem postanowiłem podzielić się swoimi doświadczeniami w dziedzinie programowania.
Czytaj dalej Matematyka w programowaniu – wstępTajemnicza liczba π
Każdy z Was na pewno już słyszał o liczbie π. Występuje ona w wielu wzorach matematycznych, np. na pole koła, objętość walca, jest przykładem liczby niewymiernej. Większość osób pamięta, że π to w przybliżeniu 3,14. Datę 14 marca zapisuje się w notacji amerykańskiej jako 3.14 i dlatego wtedy obchodzi się Dzień Liczby π. Z tej okazji piecze się okrągłe placki i dyskutuje o dziwnych właściwościach tej liczby. Po raz pierwszy Dzień Liczby π obchodzono w San Francisco w roku 1988 i uznano go oficjalnym świętem.
Dlaczego π jest tak wyjątkowa, że jako jedyna liczba ma swoje święto? Spróbujmy poznać ją trochę bliżej
Czytaj dalej Tajemnicza liczba πWzory skróconego mnożenia, trójkąt Pascala i dwumian Newtona
W szkole uczymy się m.in. następujących wzorów skróconego mnożenia.
0 (a+b)0=1
1 (a+b)1=a+b
2 (a+b)2=a2+2ab+b2
3 (a+b)3=a3+3a2b+3ab2+b3
Pamiętajmy, że a i b oznaczają dowolne wyrażenia algebraiczne lub arytmetyczne.
Jaki związek mają one z trójkątem Pascala i dwumianem Newtona?
Czytaj dalej Wzory skróconego mnożenia, trójkąt Pascala i dwumian Newtona
Złoty podział? Czym jest i gdzie go znajdziemy
Proporcjonalność jest czymś co nas otacza, znajdziemy ja w przyrodzie, w naszym ciele czy twarzach, malarstwie, matematyce czy sztuce. Nawet w gotowaniu mamy proporcje. Złoty podział jest idealnym odzwierciedleniem proporcji – boską proporcją.
Jak myśleć o matematyce?
Kilka prostych porad dla ludzi, którzy nie lubią matmy
Mówi się, że matematyka jest królową nauk. Już najwybitniejszy grecki filozof, Arystoteles mówił, iż „matematyka jest miarą wszystkiego”. Trudno z się z tym nie zgodzić – wszelkie nauki ścisłe oraz cała myśl techniczna oparte są niejako na matematyce. Nie dziwi zatem, że w szkołach na całym świecie poświęca się jej mnóstwo uwagi. Niestety, dla wielu osób jest ona przekleństwem – matematyka wymaga bowiem zrozumienia pewnych zagadnień, których znaczna część osób nie potrafi pojąć. Niemniej matematyka, przynajmniej na poziomie szkolnym jest nauką, którą zrozumieć może każdy z was. Zadaniem tego artykułu będzie odczarowanie matematyki i stworzenie modelu myślenia, dzięki któremu nawet najbardziej uprzedzona do matmy osoba będzie w stanie się z nią oswoić.
Czytaj dalej Jak myśleć o matematyce?Wszędobylska liczba π
Co jest liczba π?
Liczba π zwana inaczej ludolfiną to najpopularniejsza stała matematyczna. Definiowana jest jako stosunek obwodu koła do długości jego średnicy.
Wartość liczby π
π ≈ 3,141592653589793238462643383279502884197169…
W obliczeniach najczęściej korzysta się z przybliżonych wartości 3,14 lub 22/7.
Symbol π wprowadził walijski matematyk Williams Jones w 1706 roku, a rozpowszechnił ją Leonhard Euler.
Liczba π nazywana jest stałą Archimedesa lub ludolfiną na cześć Ludolpha van Ceulena. Obaj obliczyli wartości przybliżone liczby, Ceulenowi udało się wyznaczyć aż 35 miejsc po przecinku.
Występowanie liczby π
Liczba π występuje w geometrii, analizie matematycznej, teorii liczb, rachunku prawdopodobieństwa, wzorach demograficznych, równaniach grawitacji Einsteina, zasadzie nieoznaczoności kwantowej Heisenberga.
Najczęściej używane wzory matematyczne zawierające liczbę (na poziomie szkoły średniej)
Pole koła o promieniu r
Pole elipsy o osiach a i b
Objętość kuli o promieniu r
Pole powierzchni kuli o promieniu r
Objętość walca o wysokości H i promieniu podstawy r
Pole powierzchni walca o wysokości H i promieniu podstawy r
Liczba e występuje we wzorze Eulera zwanym „największym wzorem matematyki” wiążącym najsłynniejsze liczby.
Święto liczby π i jego znaczenie
Święto liczby π obchodzone jest 14 marca. Święto to zostało zapoczątkowane w 1988 roku przez Larry’ego Shaw, pracownika naukowego San Francisco Exploratorium, pierwszym centrum naukowym na świecie. Wybrano 14 marca ze względu na zapis dat w formacie amerykańskim (14 marca zapisuje się jako 3.14). Święto liczby π uznano za oficjalne w 2009 roku w USA, uchwałą Izby Reprezentantów.
Celem obchodów święta liczby π jest popularyzacja matematyki.
Ciekawostki
- William Shanks w XIX wieku obliczył pierwsze 707 cyfr π ręcznie, niestety popełnił błąd po 527 miejscu.
- W pierwszych 31 cyfrach po przecinku π nie ma zer.
- Najwięcej cyfr liczby π wyliczył Peter Trueb. 11 listopada 2016 roku w wyniku komputerowych obliczeń uzyskał aż 22,5 biliona cyfr po przecinku liczby π.
- Egipcjanie przybliżenie liczby π obliczali ze wzoru . Wiele budowli egipskich, z piramidami na czele, kryje dobrze przybliżoną wartość π w różnych relacjach pomiędzy wymiarami tych obiektów.
- Genialny starożytny matematyk Archimedes w celu wyliczenia przybliżenia liczby π tworzył kolejne wielokąty wpisane w okrąg oraz opisane na okręgu i obliczał ich obwody. Wykreślił on wielokąt foremny o 96 bokach. W ten sposób uzyskał następujące przybliżenie .
- π jest pierwszą literą greckiego słowa περίμετρον – perimetron, czyli obwód, obrzeże.
- Liczba π jest wspomniana w Biblii. „Następnie sporządził odlew “morza” o średnicy dziesięciu łokci, okrągłego, o wysokości pięciu łokci i o obwodzie trzydziestu łokci. (II Księga Królewska, Rozdział 7, Werset 23) Okrąg o średnicy dziesięciu łokci miał mieć obwód trzydziestu łokci, takiego przybliżenia liczby π używali Babilończycy.
- Liczba π jest liczbą niewymierną (nie można jej przedstawić jako iloraz dwóch liczb całkowitych).
- Jest liczbą przestępną (nie istnieje wielomian o współczynnikach całkowitych, którego liczba π byłaby pierwiastkiem).
- Nie można znaleźć prawdziwego obwodu lub obszaru okręgu, ponieważ nigdy nie możemy znaleźć prawdziwej wartości π.
- Średni stosunek długości doliny rzeki do długości rzeki równy dokładnie π.
- W matematyce π jest czynnikiem, występującym w wynikach licznych całek, sumach szeregów itp. Jest stosowana w rachunku z użyciem liczb urojonych.
- Liczba π jest związana z rachunkiem trygonometrycznym, który stosowany jest w elektronice, fizyce falowej, medycynie i astronomii.
- π pojawia się w rachunku prawdopodobieństwa. Np. liczba 6/ π2 to prawdopodobieństwo, że dwie losowo wygenerowane liczby nie będą miały wspólnego dzielnika innego niż jeden – czyli są liczbami pierwszymi.
- Z liczbą π związane jest nierozwiązywalne zagadnienie o nazwie kwadratura koła. Polega ono na wykreśleniu kwadratu o tej samej powierzchni co koło.
- W roku 2015 w Dniu Liczby π wystąpiła kombinacja cyfr daty i godziny, odzwierciedlająca kolejne cyfry liczby π: 3.14.15 9:26:53,58
- Około 40 cyfr po przecinku pozwala określić obwód obserwowalnego Wszechświata z dokładnością do rozmiaru pojedynczego atomu.
- NASA wystarczy nawet kilkanaście cyfr rozwinięcia liczby π, by nie zepsuć Międzynarodowej Stacji Kosmicznej i innych pojazdów/sond kosmicznych.
- Fundamentalne stałe fizyczne i matematyczne, wyliczane przez komitet CODATA, wykorzystują znajomość π do 32 cyfr po przecinku.
- Przenikalność magnetyczna próżni wynosi 4 π * 10-7.
- π występuje w stałej dielektrycznej zwanej stałą Coulomba.
- Liczba π pojawia się we wzorach na promień atomu czy rozmiar elektronu.
- π jest czynnikiem w stałej kosmologicznej i we wzorze opisującym zasadę nieoznaczoności Heisenberga.
- Liczba sekund w roku to 365·24·60·60=31 536 000 co w przybliżeniu daje π * 107*c, gdzie c oznacza prędkość światła (w kilometrach na sekundę).
- 1 rok świetlny równa się w przybliżeniu π·107·c (km).
- Uczeni szukając kontaktu z cywilizacjami pozaziemskimi, wysłali w kosmos drogą radiową informację o wartości liczby π. Wierzą, że inteligentne istoty spoza Ziemi znają tę liczbę i rozpoznają nasz komunikat.
- Aktorka, doktor matematyki Danica McKellar, zaśpiewała fragment liczby π do melodii z Dziadka do orzechów Czajkowskiego.
- 14 marca 1979 roku urodził się Albert Einstein.
MDN