Tajemnicza liczba π

Każdy z Was na pewno już słyszał o liczbie π. Występuje ona w wielu wzorach matematycznych, np. na pole koła, objętość walca, jest przykładem liczby niewymiernej. Większość osób pamięta, że π to w przybliżeniu 3,14. Datę 14 marca zapisuje się w notacji amerykańskiej jako 3.14 i dlatego wtedy obchodzi się Dzień Liczby π. Z tej okazji piecze się okrągłe placki i dyskutuje o dziwnych właściwościach tej liczby. Po raz pierwszy Dzień Liczby π obchodzono w San Francisco w roku 1988 i uznano go oficjalnym świętem.

Dlaczego π jest tak wyjątkowa, że jako jedyna liczba ma swoje święto? Spróbujmy poznać ją trochę bliżej

Czym jest liczba π i kto ją tak nazwał?

Liczba π to stosunek obwodu dowolnego koła do jej średnicy.

Oznacza to, że średnica koła mieści się w jego obwodzie π razy(czyli około 3,14). Gdybyśmy wzięli sznurek , otoczyli nim koło i odcięli resztę, a następnie rozciągnęli go na ziemi, potem wzięli patyk długości średnicy tego koła i próbowali nim zmierzyć sznurek, to otrzymalibyśmy 3 patyki i kawałek, a dokładniej mówiąc π patyka.

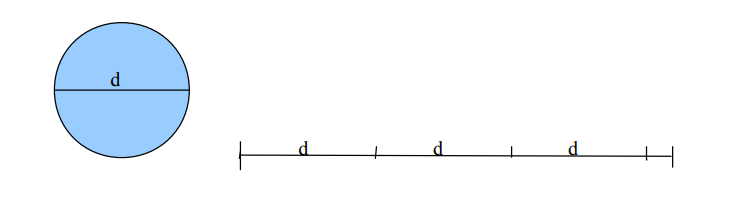
Oznaczenie liczy pi pochodzi od pierwszej litery greckiego słowa oznaczającego obwód. Używany do dziś symbol π wprowadził angielski uczony Wiliam Jones na początku XVIII wieku, a spopularyzował Leonard Euler w swoim dziele „Analiza” wydanym w 1736 roku.

Od kiedy znamy liczbę π?

Liczba ta pojawia się w Starym Testamencie przy okazji budowy świątyni Salomona. W Drugiej Księdze Kronik (Biblia Tysiąclecia , rozdział 4, werset 2) czytamy: „Następnie sporządził odlew okrągłego „morza” o średnicy dziesięciu łokci, o wysokości pięciu łokci i obwodzie 30 łokci.” Wynika stąd, że obwód koła jest trzy razy większy od średnicy.

W jednym z najstarszych pism matematycznych – egipskim papirusie Rhinda „Wprowadzenie do wiedzy o wszystkich istniejących rzeczach” pochodzącym z 1650 r. p.n.e. wartość π podano w postaci $\left ( \frac{16}{9} \right )^{2}$ , co jest równe w przybliżeniu 3,16049.

Jako pierwszy wartość liczby π z dokładnością do dwóch miejsc po przecinku obliczył najprawdopodobniej Archimedes (III w. przed Chrystusem). Stosował on metodę aproksymacji (przybliżania) opartą na zależnościach geometrycznych. Obliczał obwody wielokątów foremnych: opisanego na kole oraz wpisanego w to koło. Obwód koła miał długość mieszczącą się pomiędzy długościami obwodów tych wielokątów.

**Metoda aproksymacji Archimedesa**
źródło: By Leszek Krupinski (disputed, see File talk:Archimedes pi.svg) – Praca własna, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1250248

Archimedes wyznaczył długości obwodów dwóch 96-kątów foremnych – opisanego i wpisanego wkoło i uzyskał przedział $(3 \frac{10}{71}; 3 \frac{10}{70})$ , w którym mieści się liczba π.

Ok. 500 r. n.e chiński cesarski astronom Zu Chongzhi używając metody Archimedesa podał dwa nowe przybliżenia liczby π. Pierwsze z nich to $\frac{22}{7}$ i dlatego dzień 22 lipca jest obchodzony jako Dzień
Aproksymacji Liczby π. Drugie przybliżenie to $\frac{355}{113}$ ( co łatwo zapamiętać, bo są to liczby 11, 33, 55 w odpowiednim porządku).

Metody Archimedesa użył także niemiecki matematyk Ludolf van Ceulen, który w roku 1610 obliczył π z dokładnością do 35 miejsc po przecinku. Przybliżał on obwód koła obwodami wielokątów foremnych: wpisanego i opisanego o $2^{62}$ bokach. Po śmierci uczonego liczbę tę wyryto na jego nagrobku i zaczęto nazywać „ludolfiną”.

W XVII w porzucono geometryczne metody wyznaczania liczby π , natomiast zwrócono się w stronę ciągów nieskończonych. Najbardziej znanym przykładem szeregu związanego z π jest tzw. naprzemienny szereg Leibnitza (1674r):

$\frac{ \pi }{4} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots + \frac{(-1)^{k}}{2k-1}+ \cdots$

Dziś do poszukiwań kolejnych cyfr rozwinięcia dziesiętnego liczby π wykorzystuje się komputery. W styczniu 2010 r. francuski informatyk Fabrice Bellard ogłosił, że obliczył liczbę π z dokładnościa do prawie 2,7 bilionów miejsc po przecinku.

Jak zapamiętać wartość liczby π?

Aby ułatwić zapamiętanie wielu cyfr rozwinięcia dziesiętnego tej liczby powstają wierszyki i opowiadania , w których długość każdego kolejnego słowa jest równa kolejnej cyfrze rozwinięcia dziesiętnego. Jako pierwszy powstał wiersz Kazimierza Cwojdzińskiego (1930 r.). Uwaga: niema jest tu napisane zgodnie z pisownią sprzed wojny:

Kuć i orać                              3,14
w dzień zawzięcie.                  159
Bo plonów niema bez trudu. 26535
Złocisty szczęścia okręcie –    897
kołyszesz.                              9
Kuć!                                        3
My nie czekajmy cudu.           2384
Robota – 6
to potęga ludu!                       264
Kazimierz Cwojdziński ,,Kuć i orać”

Inny przykład:

Tak i mnie i Tobie poznawana tu liczba cudna dla ogółu przynosi wszystkim pożytek wspaniały.

Podobne wierszyki i opowiastki układane są na całym świecie w różnych językach.

Jakie są własności liczby π?

Dzięki temu, że poznaliśmy tak wiele cyfr rozwinięcia dziesiętnego liczby π , możemy przyjrzeć się jej dokładniej i badać jej własności. Okazuje się, że:

liczba π jest niewymierna – wiedzieli to już starożytni Grecy, a udowodnił ten fakt Johann Lambert w 1761 roku;
liczba π jest liczbą przestępną – czyli nie istnieje równanie wielomianowe o współczynnikach całkowitych, którego rozwiązaniem byłaby liczba π. Stąd niewymierność tej liczby jest bardziej skomplikowana niż niewymierność np. liczby √2 ;
w rozwinięciu dziesiętnym liczby π występuje każda dowolna sekwencja liczb naturalnych, np. data bitwy pod Grunwaldem pojawia się po raz pierwszy na miejscach: 7767, 7768, 7769, 7770.
liczba π prawdopodobnie jest liczbą normalną, co sugerują dwaj matematycy Dawid Bailey oraz Richard Crandall. Na czym polega normalność? Chodzi o własność, że wszystkie łańcuchy liczb o tej samej długości występują z tą samą częstością, np. 345 pojawia się tak samo często jak 980. Jednak do tej pory jeszcze tej własności w odniesieniu do rozwinięcia dziesiętnego liczby π nie udowodniono.
po obejrzeniu miliona cyfr okazało się, że częstości występowania poszczególnych cyfr są bliskie 100 000.

Gdzie pojawia się liczba π?

Oczywiście π znajdziemy w wielu wzorach matematycznych (np. na objętość walca $V = \pi r^{2} \cdot h$ ) i fizycznych (np. prędkość kątowa $\omega = 2 \pi \cdot f$ );
Liczba ta pojawia się w powiedzeniach, np. mówimy: „pi razy drzwi” lub „pi razy oko” jeśli podajemy coś w przybliżeniu, niedokładnie.
Liczba π związana jest też z problemami matematycznymi, jak np. kwadratura koła. Chodziło o to, czy da się za pomocą tylko cyrkla i linijki narysować kwadrat o polu równym polu danego koła. Dopiero w 1882 r Lindemann udowodnił, że nie da się tego zrobić i tym samym rozwiązał problem kwadratury koła.
Liczba π inspirowała wielu artystów i reżyserów. Pojawia się często w literaturze, np. w powieści „Wahadło Foucolta” autorstwa Umberto Eco. Nasza noblistka – Wisława Szymborska poświęciła tej liczbie wiersz, który znajdziecie na końcu tego artykułu. Darren Aronofsky poruszył temat tej tajemniczej liczby w swoim filmie „Pi”.

Ciekawostki

W piramidzie Cheopsa stosunek sumy dwóch boków podstawy do wysokości wynosi 3,1416. Przypadek, czy zamierzony cel budowniczych? Nie wiadomo.

Uczeni szukając kontaktu z cywilizacjami pozaziemskimi wysłali w kosmos drogą radiową informację o wartości liczby π w nadziei, że istoty pozaziemskie znają tę liczbę i rozpoznają nasz komunikat.

Eskimoskie π.
Dlaczego w Arktyce wartość π wynosi tylko 3?
Bo na zimnie wszystko się kurczy.

Mam nadzieję, że udało mi się przynajmniej w zarysie ukazać niezwykłość tej oryginalnej liczby i choć trochę zaciekawić Was jej właściwościami.

A na zakończenie wiersz Wisławy Szymborskiej:

Podziwu godna liczba Pi
trzy koma jeden cztery jeden.
Wszystkie jej dalsze cyfry też są początkowe
pięć dziewięć dwa, ponieważ nigdy się nie kończy.
Nie pozwala się objąć sześć pięć trzy pięć spojrzeniem,
osiem dziewięć obliczeniem,
siedem dziewięć wyobraźnią,
a nawet trzy dwa trzy osiem żartem, czyli porównaniem
cztery sześć do czegokolwiek
dwa sześć cztery trzy na świecie.
Najdłuższy ziemski wąż po kilkunastu metrach się urywa.
Podobnie, choć trochę później, czynią węże bajeczne.
Korowód cyfr składających się na liczbę Pi
nie zatrzymuje się na brzegu kartki,
potrafi ciągnąć się po stole, przez powietrze,
przez mur, liść, gniazdo ptasie, chmury, prosto w niebo,
przez całą nieba wzdętość i bezdenność.
O, jak krótki, wprost mysi, jest warkocz komety!
Jak wątły promień gwiazdy, że zakrzywia się w lada przestrzeni!
A tu dwa trzy piętnaście trzysta dziewiętnaście
mój numer telefonu twój numer koszuli
rok tysiąc dziewięćset siedemdziesiąty trzeci szóste piętro
ilość mieszkańców sześćdziesiąt pięć groszy
obwód w biodrach dwa palce szarada i szyfr,
w którym słowiczku mój a leć, a piej
oraz uprasza się zachować spokój,
a także ziemia i niebo przeminą,
ale nie liczba Pi, co to to nie,
ona wciąż swoje niezłe jeszcze pięć,
nie byle jakie osiem,
nie ostatnie siedem,
przynaglając, ach przynaglając gnuśną wieczność
do trwania.
Wisława Szymborska ,,Liczba Pi”

Źródła

„Matematyka przy kominku” – Michał Szurek, wyd BTC 2008
„Nowe ślady Pitagorasa. Książka o matematyce” – Bogdan Miś, wyd. btc 2011
„Księga matematycznych tajemnic” – Ian Steward Wydawnictwo Literackie 2015
http://www.math.edu.pl/liczba-pi
http://www.focus.pl/czlowiek/14-marca-swieto-liczby-pi-10975
www.matematyka.wroc.pl/doniesienia/miedzynarodowy-dzien-liczby-pi – artykuł Małgorzaty Mikołajczyk „Międzynarodowy Dzień Liczby Pi”