Liczba √2 jest prawdopodobnie najstarszą liczbą niewymierną.
Rozwinięcie √2 z dokładnością do 65 miejsca po przecinku wynosi:
1,41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799…
Dobrym przybliżeniem wymiernym √2 jest , to błąd wartości względem wartości rzeczywistej jest mniejszy niż 1/10000.
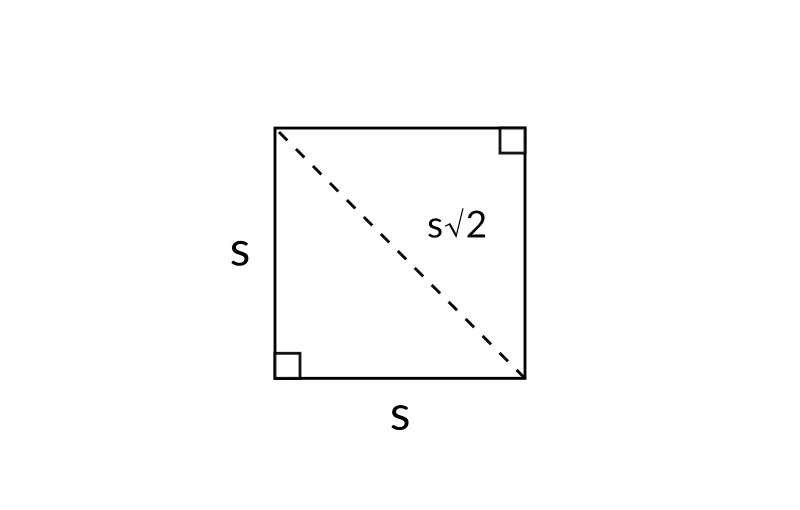
Interpretacja geometryczna liczby √2
Jeżeli zbudujemy kwadrat o długości boku 1 jednostki, to jego przekątna ma długość √2 jednostek.
Ciekawa własność liczby √2
Wiemy, że
Skorzystajmy ze wzoru skróconego mnożenia na różnicę dwóch kwadratów.
Zatem,
Czyli,
Podstawiając za otrzymujemy kolejne rozwinięcia liczby √2.
W ten sposób możemy postępować w nieskończoność.
Zastanów się, czy w podobny sposób można przedstawić liczbę √3.
Liczba √2 ma związek z kwadratem, a z jaką figurą geometryczna ma związek liczba √3?